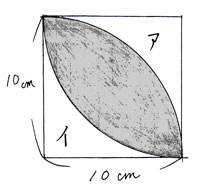
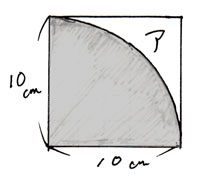
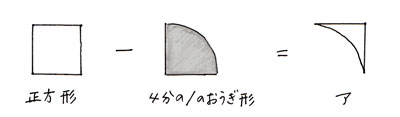
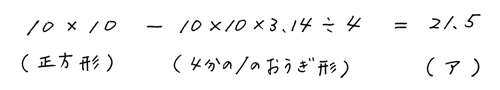
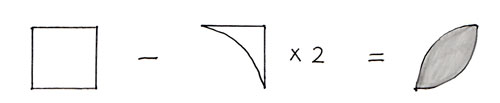
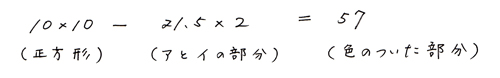
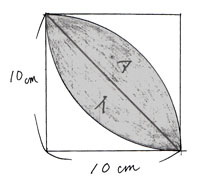
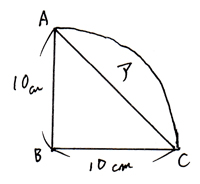
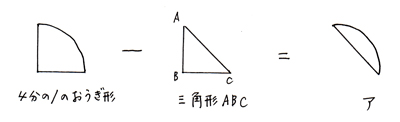
トップ 指導コラム 円の面積 応用1の解説 円の面積 応用1   円の面積の応用問題です。代表的なものから、少しだけひらめきが必要なものまでありますので、色のついた部分の面積を頑張って求めましょう。まずは代表的な問題です。ここでは3通りの求め方を解説します。 「問題1」 色のついた部分の面積を求めなさい。 「1．全体から白い部分（アとイ）を抜く方法」 アとイは同じ形なので、まずアの面積を求めましょう。 アは正方形から「色つきの部分（1/4のおうぎ形）」を引いて求めます。 これを式にすると、 イもアと同じ面積なので、アを2倍したものを全体の正方形から引くと、色のついた部分を求められます。 これを式にすると、 答え 57c㎡ 「2．色のついた部分を直接求める方法」 色のついた部分を図のように2つに分けて、まずアの面積を求めましょう。 アは1/4のおうぎ形から、三角形ABCを引いて求めます。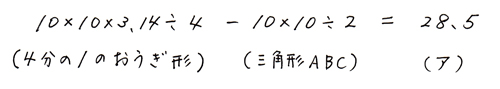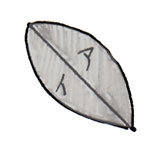 これを式にすると、 色のついた部分はアの2倍ですので、アを2倍すると色のついた部分を求められます。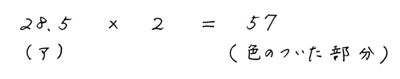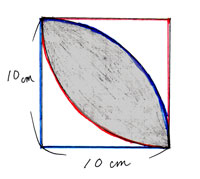 答え 57c㎡ 「3．2つのおうぎ形の重なった部分として求める方法」 ウの部分だけが2重になっていますが、ここから正方形1つ分だけを取ると重なっていた部分だけが残ります。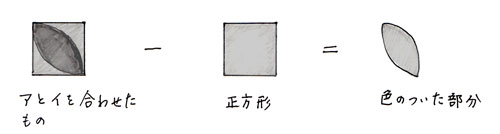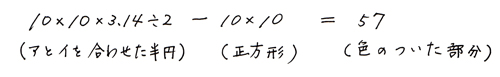 これを式にすると、 答え 57c㎡   円の面積 応用2 円の面積 応用3

｜リンク｜更新履歴｜サイトマップ｜ 〒487-0016 春日井市高蔵寺町北4-1-15 高蔵寺ファーストビル405号室 〒487-0011 春日井市中央台8-2-2 リバピア5-104   TEL/FAX：0568-91-3416　メール：info@nishimura-juku.com © Copyright by 西村セミナールーム 2013- All Rights Reserved.